Home > Games > Simulation > Conway's Game of Life
Conway's Game of Life, a fascinating creation by mathematician John Conway in 1970, is an example of a cellular automaton. This game unfolds on an infinite two-dimensional rectangular grid of cells, where each cell can be either alive or dead. The game progresses through generations, with each cell's status changing based on the statuses of its eight neighbors—those cells touching it horizontally, vertically, or diagonally.
The game begins with an initial pattern, marking the first generation. Subsequent generations evolve by applying a set of rules simultaneously to every cell on the board, leading to births and deaths occurring at the same time. These rules are iteratively applied to generate future generations. The rules governing the transition from one generation to the next are straightforward yet profound:
- If a cell is alive, it remains alive in the next generation if it has either 2 or 3 live neighbors.
- If a cell is dead, it becomes alive in the next generation only if it has exactly 3 live neighbors.
John Conway experimented with numerous variations of these rules, adjusting the numbers that determine when cells live or die. Some variations led to quick population extinction, while others resulted in unchecked expansion across the grid. The chosen rules strike a delicate balance near the boundary between these extremes, fostering complex and intriguing patterns. This balance is akin to other chaotic systems where the most interesting dynamics occur at the edge of stability and chaos.
What's New in the Latest Version 0.2.2
Last updated on Aug 3, 2024
Additional Game Information
Latest Version0.2.2 |
Category |
Requires AndroidAndroid 5.0+ |
Available on |
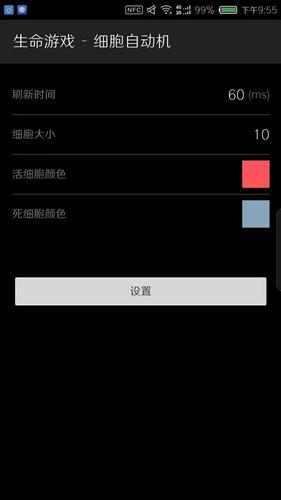
Conway's Game of Life Screenshots
Top Download
More >Trending games
-

- Learning Basic of Al-Qur'an
- 3.6 Educational
- This app simplifies Quranic recitation learning for all ages, especially children. Its engaging design, including animations and audio, motivates users to learn. The app's learning materials cover: Hijaiyah alphabet Harakat (Fathah, Kasrah, Dammah) Tanwin Mad (prolongation) Tajweed rules (Idgham,
-

-

- A Camp with Mom and My Annoying Friend Who Wants To Rail Her
- 4.3 Casual
- Immerse yourself in "A Camp with Mom and My Annoying Friend" on your 2-day camping adventure. Interact with Souma, Kyouko, and Kengo as they navigate unexpected twists and turns. Enjoy stunning animated scenes and explore 15 captivating scenarios in English, Chinese, or Japanese. Experience the unfiltered version for an authentic gaming experience.
-

- Top Football Manager 2024 Mod
- 4.2 Sports
- Unleash your soccer management dreams with Top Football Manager 2024! Guide your team to greatness, bid on top players, and compete against global managers. Immerse yourself in stunning 3D graphics and experience real-time matches. Strategy and betting bring you closer to becoming a champion. Build your legendary team now!
-

- Camp With Mom
- 4.2 Simulation
- Embark on a magical camping adventure with Camp With Mom! Immerse yourself in enchanted forests, solve puzzles, and connect with your mother. Experience a heartwarming story and stunning graphics that bring the game to life. Download now for an unforgettable journey!
-

- Quiz Tabuada Facil
- 4 Puzzle
- Quiz Tabuada Fácil: Test Your Multiplication Skills!Challenge yourself with Quiz Tabuada Fácil, the ultimate multiplication game. With varying difficulty levels, it's perfect for solo or multiplayer fun. Learn and master times tables while having a blast. Download now for free!
Latest Games
-

- Enchanted Hearts
- 4.6 Simulation
- Enchanted Hearts immerses players in a captivating mobile game that combines self-discovery, love, and supernatural intrigue. As the story begins, you’ll encounter a perilous situation involving a stranger, sparking the discovery of latent magical abilities tied to a lineage of powerful witches and
-

- Rudra Cooking Restaurant Game
- 4.0 Simulation
- Rudra Cooking Restaurant Game is a lively and immersive cooking adventure that brings players into the heart of a bustling kitchen alongside Rudra and his friends. This engaging title blends time management, culinary creativity, and smooth gameplay to deliver an experience suitable for players of al
-

- Oppa doll
- 4.3 Simulation
- Unnie Doll delivers a refreshing and accessible approach to fashion for those who appreciate beauty and creative expression. Whether you're uncertain about matching outfits and accessories or simply enjoy experimenting with styles based on your instincts, this platform offers the perfect playground
-

- SpongeBob Adventures: In A Jam
- 4.8 Simulation
- Transform Bikini Bottom into a paradise Dive into SpongeBob Adventures, where players take on the exciting challenge of rebuilding and customizing Bikini Bottom after Plankton’s chaotic mishap leaves it in disarray. Step into the shoes of SpongeBob and his friends as you explore, restore, and decor
-

- Bermuda Adventures Farm Island
- 4.3 Simulation
- Embark on an exhilarating journey through Bermuda Adventures, where you'll dive headfirst into the vibrant tapestry of island life. As the sole survivor of a mysterious plane crash, you find yourself stranded on a lush tropical island teeming with hidden wonders and untold secrets. Your mission? To
-

- F150 Truck Game Racing 2024
- 3.6 Simulation
- Why Should You Choose F150 Truck Game Racing 2024 as Your First Option?Step into the exhilarating world of car simulations with F150 Truck Game Racing 2024. This game stands out as the premier choice for mobile offline racing experiences. Designed for those who crave thrilling races without relying
-

- Dino Factory
- 4.8 Simulation
- Building your dream Dino Factory As the sun rises over the lush and untamed terrain of Virant Dino World—a realm where time stands still and dinosaurs once again roam free—you step into an exhilarating new role. You are now the mastermind behind the Dino Factory, a dynamic enterprise where you can b
-

- ePSXe for Android
- 4.1 Simulation
- ESXe is a closed-source, plugin-based cross-platform PlayStation emulator that has been delighting retro gaming enthusiasts for years. Developed by Calb, Galtor, and Demo, this powerful software revives the best of the PS1 gaming era on modern devices, including Windows, MacOS, Linux, and Android sy
-

- Valet Master - Car Parking
- 4.0 Simulation
- Dive into a world where precision driving blends seamlessly with strategic thinking. With diverse challenges and adjustable difficulty levels, *Valet Master Car Parking* is designed to sharpen your parking skills like never before. Maneuver through narrow spaces, dodge obstacles, and execute flawles